Программирование управляющих программ станка с системой ЧПУ 2С42. стр.32.

2.4. Круговая интерполяция.

       Круговая интерполяция задаётся функциями G02 или G03.
       Перемещение по дуге окружности в плоскости XY.
       G17G02(G03) X_Y_I_J_F_
       По дуге окружности в плоскости ZX
       G18G02(G03)X_Z_I_K_F_
       По дуге окружности в плоскости YZ
       G19G02(G03)Y_Z_J_K_F_

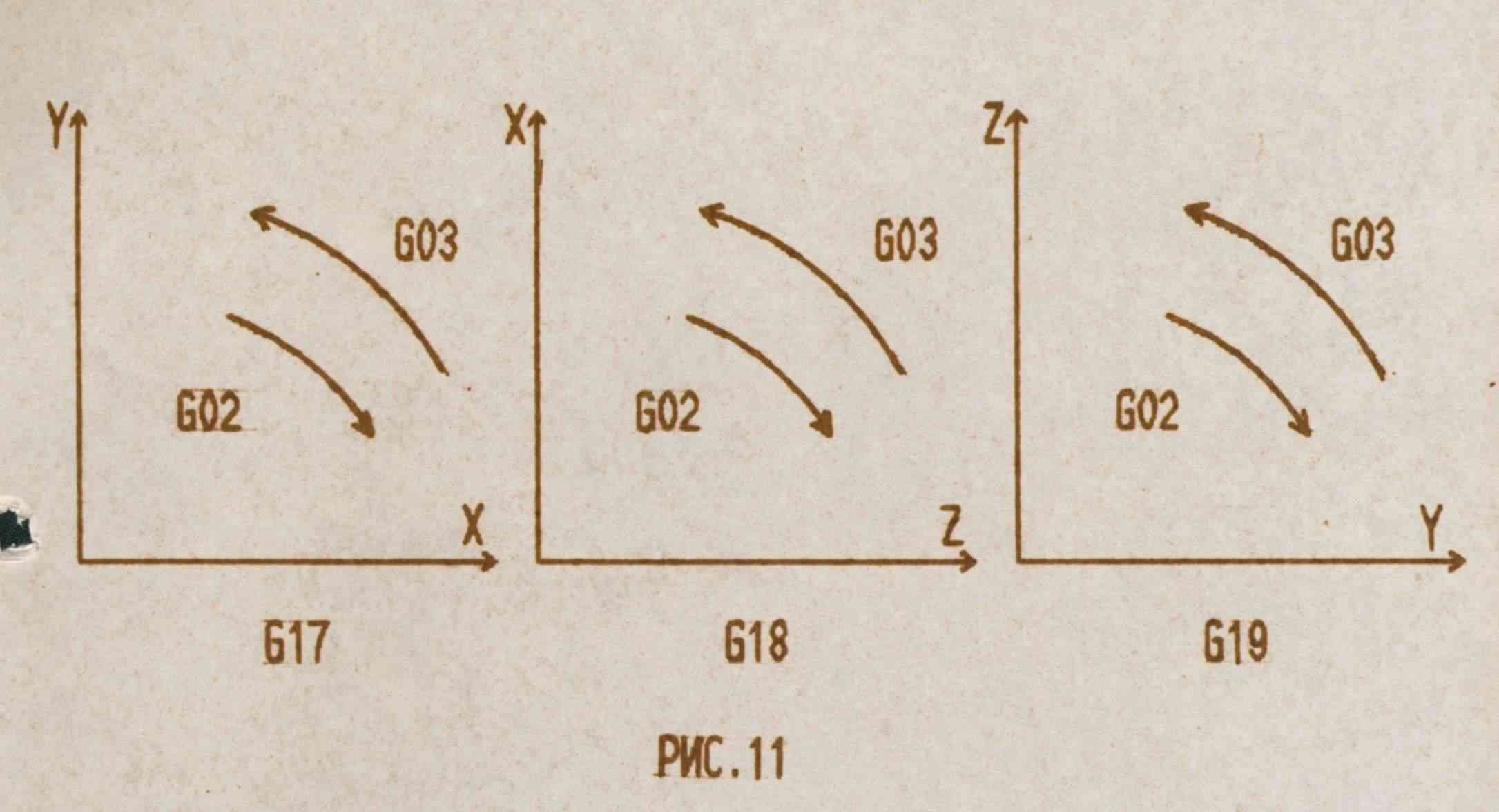
В Таблице 8 расшифровывается смысл функций и адресов, используемых при программировании круговой интерполяции.

	ЗАДАНИЕ	КОД	СМЫСЛ
1	ЗАДАНИЕ ПЛОСКОСТИ	G17	ЗАДАНИЕ ДУГИ ОКРУЖНОСТИ НА ПЛОСКОСТИ XY
		G18	ЗАДАНИЕ ДУГИ ОКРУЖНОСТИ НА ПЛОСКОСТИ ZX
		G19	ЗАДАНИЕ ДУГИ ОКРУЖНОСТИ НА ПЛОСКОСТИ YZ
2	НАПРАВЛЕНИЕ ВРАЩЕНИЯ	G02	ПО ЧАСОВОЙ СТРЕЛКЕ
2	НАПРАВЛЕНИЕ ВРАЩЕНИЯ	G03	ПРОТИВ ЧАСОВОЙ СТРЕЛКИ
3	ПОЛОЖЕНИЕ КОНЕЧНОЙ ТОЧКИ	G90	ПОЛОЖЕНИЕ КОНЕЧНОЙ ТОЧКИ В КООРДИНАТНОЙ СИСТЕМЕ
4	РАССТОЯНИЕ ОТ НАЧАЛЬНОЙ ТОЧКИ ДО ЦЕНТРА	ДВЕ ИЗ КООРДИНАТ I, J, K	РАССТОЯНИЕ ОТ НАЧАЛЬНОЙ ТОЧКИ ДО ЦЕНТРА СО ЗНАКОМ

Направление по часовой стрелке и против часовой стрелки определяется, если смотреть

       На плоскость XY с положительного направления Z в отрицательное
       На плоскость ZX с положительного направления Y в отрицательное
       На плоскость YZ с положительного направления X в отрицательное

Смотри Рис. 11.

Программирование векторов I, J, K определяющих положение центра дуги начальной точки осуществляется всегда в приращениях, независимо от G90 или G91.

В зависимости от направления I, J, K необходимо выбрать для них соответствующий знак.

Пример программы: Смотри Рис. 12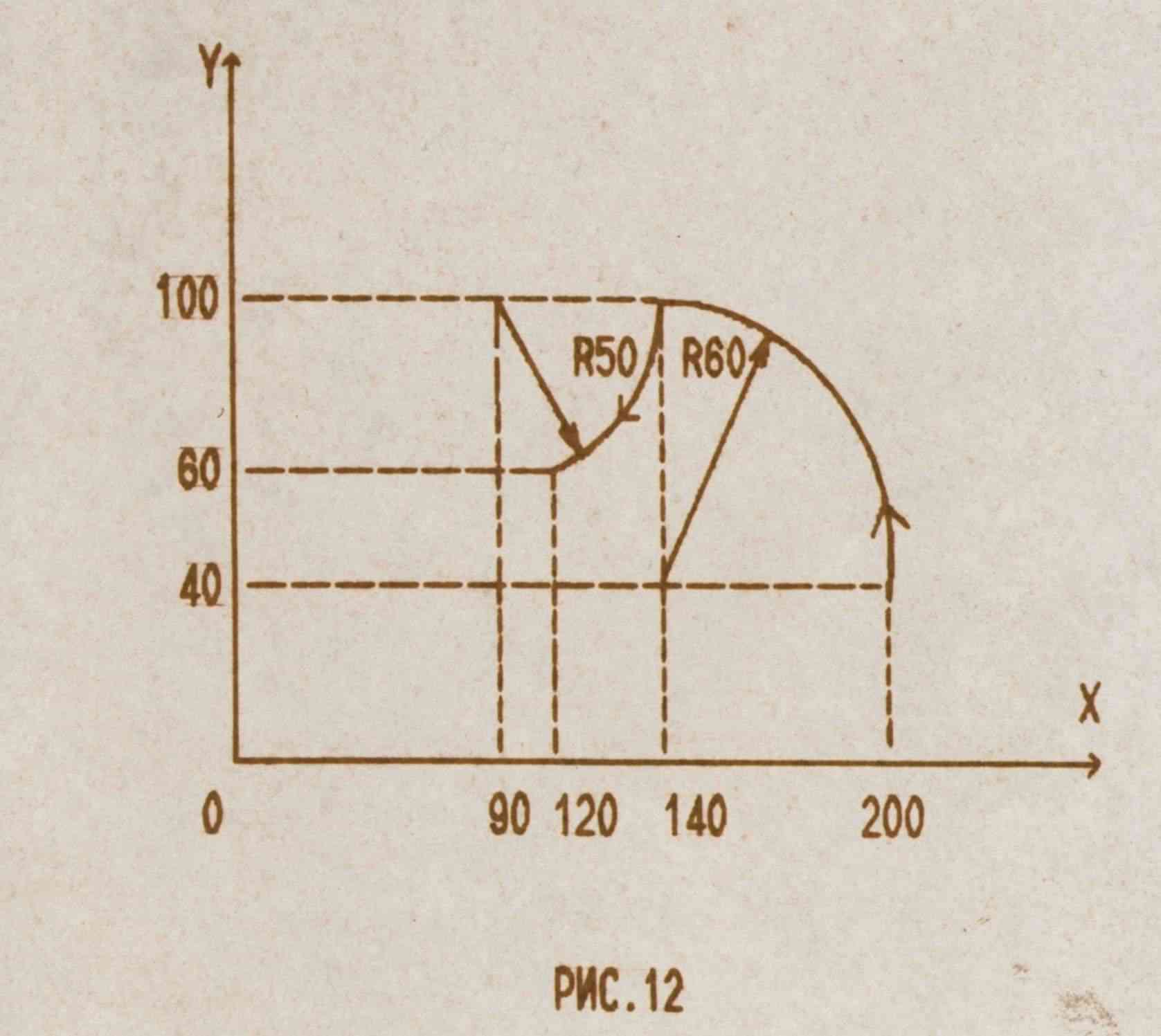

       В абсолютных величинах:
       NG92X200Y40Z0
       NG90G17G03X140Y100I-60F300
       NG02X120Y60I-50
       В приращениях:
       NG91G17G03X-60Y60I-60F300
       NG02X-20Y-40I-50

Скорость подачи для круговой интерполяции соответствует заданной величине F, направлена по касательной к дуге окружности и поддерживается постоянной в каждой точке дуги.

Примечание:

Если задан центр с использованием векторов I, J, K и не задан ни один из адресов X, Y, Z, то это соответствует заданию дуги окружности на 360 град. (задание полной окружности).